Bäume

6. Bäume#

Bäume sind eine der wichtigsten Datenstrukturen, die es in der Informatik gibt. In diesem Kapitel erfährst du

  • wozu man Bäume verwendet

  • wie man mit Bäumen arbeitet, also wie man mit Bäumen Informationen speichern, verarbeiten und abrufen kann

  • wie man sie modelliert und implementiert.

6.1. Bäume sind in der Informatik überall#

Sieh dir die folgenden Abbildungen an. Welche Zusammenhänge werden hier dargestellt? Was drücken die Knoten und Kanten der Bäume jeweils aus?

../_images/baum_saeugetiere.svg

Abb. 6.1 Klassifikation von Säugetieren (sehr unvollständig 😉)#

../_images/Binaerer_Suchbaum_15_Knoten.svg

Abb. 6.2 Ein binärer Suchbaum. Enthält er den Wert 12?#

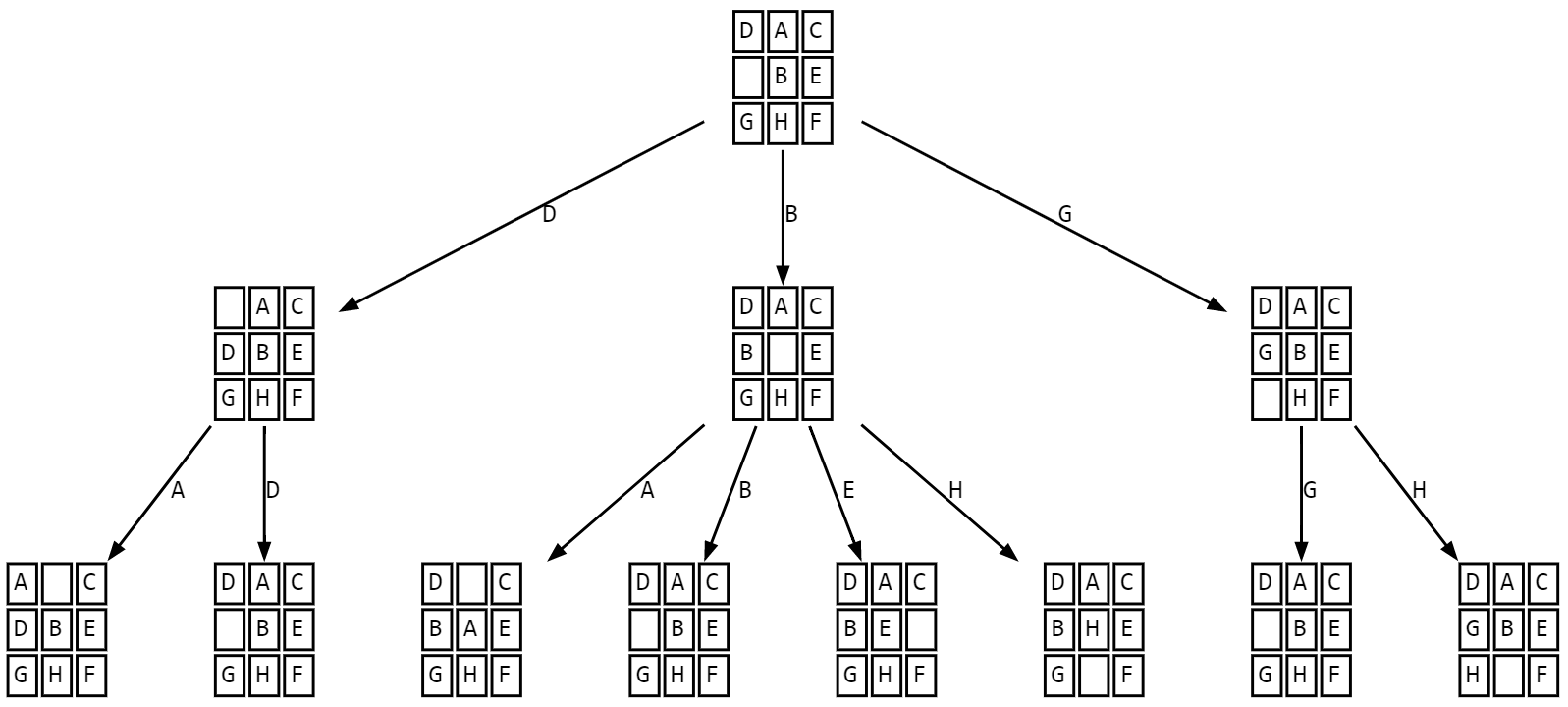
../_images/breitensuche_suchbaum01.png

Abb. 6.3 Spielbaum für ein Schiebepuzzle (nur ein winziger Ausschnitt)#

../_images/term.svg

Abb. 6.4 Dieser Baum stellt einen Rechenausdruck (Term) dar. Welche Zahl ergibt sich, wenn man ihn berechnet?#

Auch das folgende HTML-Dokument hat eine Baumstruktur. Erkläre, wieso!

<html>
<head>
    <meta charset="UTF-8">
    <title>ChatGPT</title>
</head>
<body>
    <header>
        <h1>ChatGPT - Die Zukunft der Kommunikation</h1>
    </header>
    <div class="container">
        <h2>Willkommen zur ChatGPT-Revolution</h2>
        <p>
            ChatGPT ist eine bahnbrechende KI-Technologie, die natuerliche menschliche Kommunikation ermoeglicht. Egal, ob Sie Fragen beantworten moechten, Texte generieren oder Unterhaltungen fuehren - ChatGPT steht Ihnen zur Verfuegung.
        </p>
        <p>
            Diese HTML-Seite dient nur zur Veranschaulichung des Themas ChatGPT. Sie koennen ChatGPT in verschiedenen Anwendungen wie Chatbots, Kundenbetreuung und mehr verwenden.
        </p>
        <p>
            Die Zukunft der Kommunikation ist hier, und ChatGPT ist ein wichtiger Teil davon!
        </p>
    </div>
</body>
</html>

Aufgabe: Stelle die HTML-Struktur als Baum dar. Dein Ergebnis sollte der Tier-Taxonomie in Abb. 6.1 ähneln.

Lösung

../_images/html_baum.svg

Abb. 6.5 Baumstruktur für ein HTML-Dokument#

6.2. Wichtige Begriffe im Zusammenhang mit Bäumen#

Die folgende Abb. 6.6 und der nachstehende Text für einige wichtige Begriffe ein, die du kennen musst, um über Bäume sprechen zu können.

../_images/Baum.svg

Abb. 6.6 Wichtige Begriffe zur Beschreibung von Baumstrukturen#

Wichtig

Ein Baum besteht aus einer Menge von Knoten, die untereinander durch Kanten verbunden sind. Ein bestimmter Knoten bildet die Wurzel des Baums; der Wurzelknoten hat keine eingehende Kante, d.h.h. keinen Vorgänger. Die Knoten, von denen keine Kanten mehr ausgehen, werden Blätter oder äußere Knoten des Baums genannt. Die anderen Knoten, von denen Kanten ausgehen, heißen innere Knoten. Der Vorgänger eines Knoten kann als Elternknoten und die Nachfolger eines Knoten als Kindknoten bezeichnet werden. Aus diesem Grund hat jeder Knoten im Baum, außer dem Wurzelknoten, genau einen Elternknoten.

Für einen Baum gelten folgende zwei Regeln:

  1. Es gibt genau einen Knoten ohne Vorgänger und das ist die Wurzel.

  2. Jeder andere Knoten hat genau einen Vorgänger.

Als Pfad in einem Baum wird der Weg über Kanten des Baums bezeichnet, die man gehen muss, um von einem Knoten zu einem anderen Knoten zu gelangen. Die Länge eines Pfads ist die Anzahl der Kanten auf dem Pfad.
Bemerkung: In einem Baum ist es unmöglich im Kreis zu laufen oder den Ausgangsknoten wieder zu erreichen.

Ausgehend von der Wurzel kann man die Knoten eines Baums in Ebenen einteilen. Alle Knoten mit dem gleichen Abstand (d.h. Pfadlänge) zur Wurzel liegen in derselben Ebene.

Die Tiefe eines Baums entspricht der Anzahl der Knoten im längsten Pfad des Baums.

Ein Binärbaum ist ein Baum, bei dem jeder Knoten maximal zwei Nachfolger hat.

Ein Suchbaum ist ein Baum, in dem die Knoten auf eine bestimmte Weise so angeordnet sind, dass man bestimmte Werte im Baum sehr finden kann (s. späteres Kapitel). Ein binärer Suchbaum ist ein Suchbaum, bei dem jeder Knoten maximal zwei Nachfolger hat.

6.3. Aufgaben#

6.3.1. Begrifflichkeiten richtig anwenden#

Betrachte den Baum in Abb. 6.7 und beantworte dann die folgenden Fragen:

../_images/zahlen_aufgabe_begriffe.svg

Abb. 6.7 Ein Baum voller Zahlen#

Zähle alle Blätter des Baums auf.

4, 5, 8, 13, 10, 11, 12

Welcher Knoten ist der Elternknoten von Knoten 5?

2

Zähle die Kindknoten von Knoten 3 auf.

6 und 7

Beschreibe den Pfad von Knoten 3 zu Knoten 13. Gib dazu die Knoten auf dem Pfad an.

3, 7, 9, 13

Welche Tiefe hat der Baum?

4

Auf welcher Ebene liegt der Knoten 6? Auf welcher der Knoten 1?

Knoten 6 liegt auf Ebene 2.
Knoten 1 liegt auf Ebene 0.

Welche Knoten liegen auf Ebene 3?

8, 9, 10, 11, 12

Zusatzfrage: Wie kann man am einfachsten prüfen, ob es einen Pfad vom Knoten 2 zum Knoten 13 gibt?

Am einfachsten ist es, wenn man vom Ende des gesuchten Pfads (hier: Knoten 13) aus sucht: Man geht rückwärts zum Vorgänger (hier: Knoten 9), dann zu dessen Vorgänger (hier: Knoten 7) usw., bis man entweder den gesuchten Anfang des möglichen Pfads gefunden hat oder bei der Wurzel gelandet ist (das ist in diesem Beispiel der Fall).

6.3.2. Baum oder kein Baum?#

Begründe, welche der untenstehenden Strukturen einen Baum darstellen und welche nicht.

../_images/baum_nichtbaum.svg

Abb. 6.8 Baum oder nicht Baum - das ist hier die Frage!#

Lösungen:

a. kein Baum
b. kein Baum
c. Baum
d. Baum
e. kein Baum
f. Baum
g. Baum
h. kein Baum

Inhalt