9. Der k-Nächste-Nachbarn-Algorithmus#
Der k-Nächste-Nachbarn-Algorithmus klassifiziert
einen bisher ungelabelten Datensatz, indem er ihn mit seinen “nächsten Nachbarn” vergleicht, d.h. mit
denjenigen bereits gelabelten Datensätzen, die dem neuen Datensatz am ähnlichsten sind.
Dem unbekannten Datensatz wird dann dasjenige Label zugeordnet, das die Mehrheit der “Nachbarn” hat.
Klingt kompliziert? Keine Sorge - das Verfahren ist total einfach. Am folgenden interaktiven Beispiel wirst du schnell verstehen, wie der k-Nächste-Nachbarn-Algorithmus funktioniert.
9.1. Einführung: Tiere klassifizieren#
Interaktives Ausprobieren des k-NN-Verfahrens: Bewege deinen Mauszeiger über die Darstellung unten. Jede Position entspricht einem Tier mit einer gewissen Niedlichkeit und Flauschigkeit. Klicke an eine Position um zu sehen, in welche Kategorie der kNN-Algorithmus dieses Tier einordnen würde. Klicke erneut, um eine neue Position zu suchen.
Aufgabe 1:
Finde durch Ausprobieren heraus, wie die folgenden Tiere klassifiziert werden:
ein Tier mit Niedlichkeit 0,57 und Flauschigkeit 0,71
ein Tier mit Niedlichkeit 0,33 und Flauschigkeit 0,93
ein Tier mit Niedlichkeit 0,22 und Flauschigkeit 0,17
Als welche Spezies wird vermutlich ein Tier mit Niedlichkeit 0,62 und Flauschigkeit 0,48 klassifiziert? Überlege zuerst und überprüfe dann deine Vermutung durch einen Klick an die entsprechende Position.
Wenn einer Position (d.h. einem neuen, unbekannten Tier) eine Kategorie zugeordnet wird, erscheinen Linien zu anderen Tieren. Diskutiere mit deiner Sitznachbarin, was diese Linien bedeuten?
Warum wird der Datenpunkt
(0,51/0,38)mit einem Fragezeichen angezeigt, d.h. warum kann er nicht kategorisiert werden?Wie wird ein Tier mit Niedlichkeit 0,50 und Flauschigkeit 0,50 kategorisiert? Was ändert sich, wenn du den Wert von \(k\) auf 4 änderst, aber die Position beibehältst. Erkläre!
Probiere auch alle anderen möglichen Werte für \(k\) aus. Erkläre, was passiert.
Welchen der möglichen Werte für \(k\) würdest du wählen, um eine möglichst gute Klassifikation zu erhalten?Schreibe in 1-2 Sätzen auf, wie der k-Nächste-Nachbarn-Algorithmus deiner Meinung nach arbeitet. Vergleiche deine Definition mit der deiner Sitznachbarin.
Lösungen
Durch Klicken an die entsprechenden Positionen findet man:
Kaninchen
Vogelspinne
Hai
Man vermutet evtl Kaninchen, weil das nächstegelegene Tier ein Kaninchen ist, aber der Punkt wird als Igel klassifiziert. (Weil von den 5 nächstgelegenen Tieren 3, also die Mehrheit, Igel sind.)
Die Linien zeigen die \(k\) am nächsten gelegenen Tiere (die “Nachbarn” des angeklickten Punkts), wobei \(k\) die Zahl ist, die im Auswahlfeld unten gewählt wurde.
Unter den 5 nächsten Nachbarn kommt keine Spezies eindeutig am häufigsten vor, d.h. keine Spezies hat eine eindeutige Mehrheit. (Unentschieden zwischen 2 Haien und 2 Igeln).
Für k=5: Vogelspinne, aber für k=4: Fragezeichen. Erklärung: Es gibt bei k=4 keine eindeutige Mehrheit untern den Nachbarn, d.h. keine Tierart, die am häufigsten unter den Nachbarn vorkommt.
Es werden jeweils die \(k\) nächsten Nachbarn angezeigt. Für k=1 wird nur der nächste Nachbar angezeigt, für k=2 die zwei nächsten Nachbarn, usw. Für k=5 wird die Mehrheit der 5 nächsten Nachbarn angezeigt.
Sinnvolles \(k\) auswählen: k=1 ist zu wenig, weil ein einzelner Nachbar nicht unbedingt repräsentativ ist (Ausreißer). Ein großes \(k\) robuster, aber dadurch geht unter Umständen die Genauigkeit verloren, weil “örtliche Besonderheiten” nicht mehr berücksichtigt werden. In unserem Beispiel würde z.B. k=20 bedeuten, dass es vollkommen egal wird, wohin man klickt.Eine mögliche Beschreibung des Verfahrens in zwei Sätzen findest du am Anfang des nächsten Abschnitts.
9.2. Intuitive Beschreibung des Algorithmus#
Wichtig
Umgangssprachlich kann der k-Nächste-Nachbarn-Algorithmus so beschrieben werden: Um einen ungelabelten Datensatz zu klassifizieren
finde die \(k\) Datensätze, die dem ungelabelte Datensatz am ähnlichsten sind.
gib das Label zurück, das in diesen \(k\) Datensätzen am häufigsten vorkommt.
9.3. Programmierung des Algorihmus (1)#
9.3.1. Beispieldaten vorbereiten#
trainingsdaten = """
niedlichkeit, flauschigkeit, spezies
0.21, 0.91, vogelspinne
0.27, 0.8, vogelspinne
0.15, 0.75, vogelspinne
0.37, 0.87, vogelspinne
0.29, 0.7, vogelspinne
0.9, 0.9, kaninchen
0.86, 0.8, kaninchen
0.75, 0.84, kaninchen
0.95, 0.75, kaninchen
0.7, 0.65, kaninchen
0.31, 0.22, hai
0.14, 0.13, hai
0.21, 0.06, hai
0.11, 0.25, hai
0.33, 0.11, hai
0.9, 0.1, igel
0.8, 0.17, igel
0.7, 0.11, igel
0.75, 0.26, igel
0.92, 0.22, igel
"""
9.3.2. Daten in Objekte der Klasse Tier einlesen#
class Tier:
def __init__(self, niedlichkeit: float, flauschigkeit: float, spezies: str) -> None:
self.niedlichkeit: float = niedlichkeit
self.flauschigkeit: float = flauschigkeit
self.spezies: str = spezies
def __repr__(self) -> str:
return f"Tier({self.niedlichkeit}, {self.flauschigkeit}, '{self.spezies}')"
def kopie_mit_spezies(self, neue_spezies: str) -> Tier:
return Tier(self.niedlichkeit, self.flauschigkeit, neue_spezies)
def __lt__(self, other) -> bool:
return True # Tiere sind eigentlich nicht vergleichbar; wir müssen aber irgendeine Implementierung angeben für die Sortierung später
def tier_einlesen(zeile: str) -> Tier:
niedlichkeit, flauschigkeit, spezies = zeile.strip().split(", ")
return Tier(float(niedlichkeit), float(flauschigkeit), spezies)
def tiere_aus_tabelle_einlesen(daten: str) -> list[Tier]:
tiere = []
zeilen = daten.strip().split("\n")
for zeile in zeilen[1:]: # 1. Zeile ist Überschrift, also überspringen
tiere.append(tier_einlesen(zeile))
return tiere
tiere = tiere_aus_tabelle_einlesen(trainingsdaten)
print(tiere) # Ausgabe: [Tier(0.21, 0.91, 'vogelspinne'), Tier(0.27, 0.8, 'vogelspinne'), ...]
[Tier(0.21, 0.91, 'vogelspinne'), Tier(0.27, 0.8, 'vogelspinne'), Tier(0.15, 0.75, 'vogelspinne'), Tier(0.37, 0.87, 'vogelspinne'), Tier(0.29, 0.7, 'vogelspinne'), Tier(0.9, 0.9, 'kaninchen'), Tier(0.86, 0.8, 'kaninchen'), Tier(0.75, 0.84, 'kaninchen'), Tier(0.95, 0.75, 'kaninchen'), Tier(0.7, 0.65, 'kaninchen'), Tier(0.31, 0.22, 'hai'), Tier(0.14, 0.13, 'hai'), Tier(0.21, 0.06, 'hai'), Tier(0.11, 0.25, 'hai'), Tier(0.33, 0.11, 'hai'), Tier(0.9, 0.1, 'igel'), Tier(0.8, 0.17, 'igel'), Tier(0.7, 0.11, 'igel'), Tier(0.75, 0.26, 'igel'), Tier(0.92, 0.22, 'igel')]
9.3.3. Daten visualisieren#
# Visualisierung
import matplotlib.pyplot as plt
spezies_zu_farbe = {
"vogelspinne": "red",
"kaninchen": "blue",
"hai": "green",
"igel": "brown",
"?": "black"
}
def plotte_daten(alle: list[Tier], unbekanntes_tier: Tier = None, auswahl: list[Tier]=[]) -> None:
""" Visualisiert die Tiere in einem Diagramm.
Falls der zweite und dritte Parameter gegeben sind, werden das unbekannte Tier und die ausgewählten Tiere
durch Linien verbunden.
"""
fig, ax = plt.subplots(figsize=(6, 6))
plt.xlabel("Niedlichkeit")
plt.ylabel("Flauschigkeit")
ax.set_xlim(0, 1)
ax.set_ylim(0, 1)
ax.set_aspect('equal', adjustable='box')
# Ausgewählte Tier mit Linien zum unbekannten Tier verbinden
for tier in auswahl:
plt.plot([unbekanntes_tier.niedlichkeit, tier.niedlichkeit], [unbekanntes_tier.flauschigkeit, tier.flauschigkeit], color="black", linestyle="--", linewidth=0.5)
# Alle Tiere plotten
if unbekanntes_tier != None and unbekanntes_tier not in alle:
alle = alle + [unbekanntes_tier]
for tier in alle:
buchstabe = tier.spezies[0].upper()
farbe = spezies_zu_farbe[tier.spezies]
plt.text(tier.niedlichkeit, tier.flauschigkeit, buchstabe, color=farbe, fontsize=12, ha='center', va='center')
plt.show()
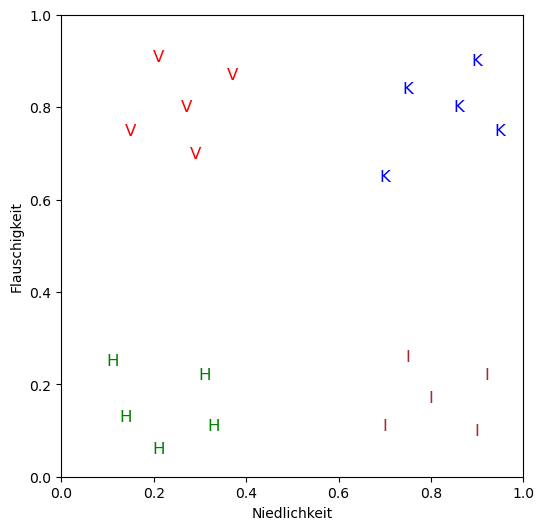
plotte_daten(tiere)
9.3.4. Einen (noch) ungelabelten Datensatz vorbereiten und anzeigen#
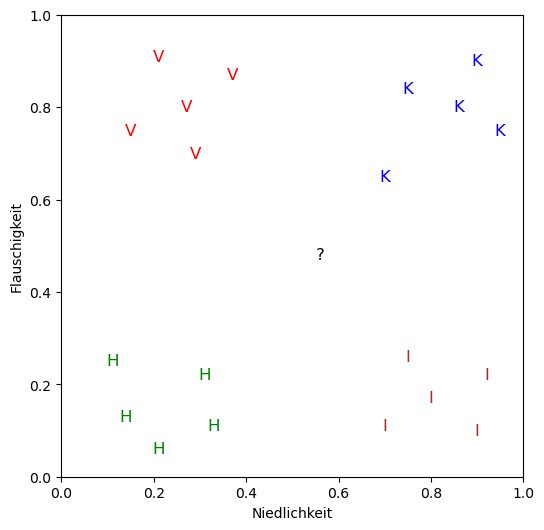
unbekanntes_tier = Tier(niedlichkeit=0.56, flauschigkeit=0.48, spezies="?") # Fragezeichen für unbekannte Spezies
# plotte Daten und das unbekannte Tier
plotte_daten(tiere + [unbekanntes_tier])
9.4. Ähnlichkeit als Distanz#
Um herauszufinden, zu welcher Spezies das neue Tier gehört, müssen wir “ähnliche” Tiere finden. Die entscheidende Idee hierbei ist, dass wir Ähnlichkeit als Distanz zwischen den Datenpunkten definieren: Jedes Tier ist charakterisiert durch zwei Merkmale (Niedlichkeit und Flauschigkeit). Diese beiden Werte definieren einen Punkt im zweidimensionalen Raum. Je kleiner der Abstand zwischen zwei Punkten, desto ähnlicher sind die beiden Tiere. Wenn wir noch mehr Merkmale hätten, könnten wir den Raum entsprechend erweitern, also z.B. bei drei Merkmalen den Abstand zwischen zwei Punkten im dreidimensionalen Raum berechnen.
9.4.1. Euklidische Distanz#
Es gibt verschiedene Definitionen für den Abstand zwischen zwei Punkten. Du kennst schon lange den sogenannten euklidischen Abstand, der zwischen zwei Punkten \(P(x_P, y_P)\) und \(Q(x_Q, y_Q)\) in der Ebene wie folgt definiert ist:
also über den Satz des Pythagoras. Für mehrdimensionale Räume gibt es eine Verallgemeinerung, die du auch in der Formelsammlung findest:
Wir setzen diese Definition als Python-Funktion um und lassen uns ein paar Distanzen anzeigen:
# Wir setzten diese Definition als Python-Funktion um und lassen uns ein paar Distanzen anzeigen:
def euklidische_distanz(tier1: Tier, tier2: Tier) -> float:
d_niedlichkeit = tier1.niedlichkeit - tier2.niedlichkeit
d_flauschigkeit = tier1.flauschigkeit - tier2.flauschigkeit
distanz = (d_niedlichkeit**2 + d_flauschigkeit**2) ** 0.5 # Pythagoras! (Erinnere dich: "hoch 1/2" = "Wurzel")
return distanz
# Test: Wir vergleichen das unbekannte Tier mit einigen anderen aus der Liste
# Wir wählen vier beliebige Tiere aus, die wir vergleichen wollen
auswahl = [tiere[3], tiere[9], tiere[10], tiere[15]]
print(f"Von unserem unbekannten {unbekanntes_tier} zum...")
for tier in auswahl:
distanz = euklidische_distanz(unbekanntes_tier, tier)
print(f" {tier} beträgt die euklidische Distanz {distanz:.2f}")
Von unserem unbekannten Tier(0.56, 0.48, '?') zum...
Tier(0.37, 0.87, 'vogelspinne') beträgt die euklidische Distanz 0.43
Tier(0.7, 0.65, 'kaninchen') beträgt die euklidische Distanz 0.22
Tier(0.31, 0.22, 'hai') beträgt die euklidische Distanz 0.36
Tier(0.9, 0.1, 'igel') beträgt die euklidische Distanz 0.51
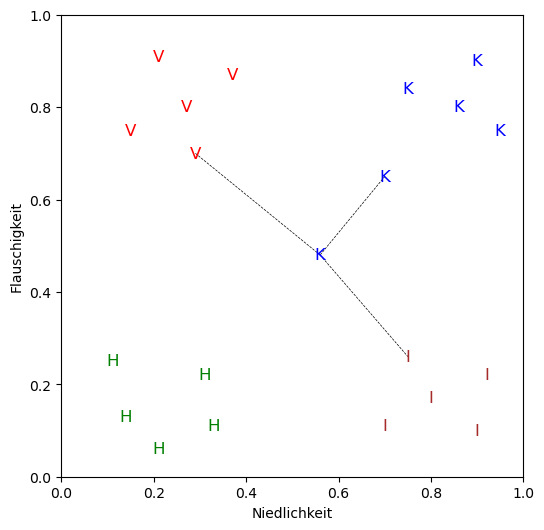
Praktischerweise kann die Funktion plotte_daten() auch Distanzen als Linien darstellen:
plotte_daten(tiere, unbekanntes_tier, auswahl)
Du siehst hier die einige Distanzen zu unserem unbekannten Tier dargestellt. Da wir aber einfach irgendwelche Tiere ausgewählt haben, sind es nicht immer die nächsten Nachbarn des unbekannten Tiers. Im nächsten Schritt müssen wir also diese nächsten Nachbarn finden, also diejenigen Datenpunkte, die die kürzesten Distanzen zu unserem unbekannten Tier haben.
Bevor wir das tun, schauen wir uns aber noch eine andere Art der Ähnlichkeits- bzw. Distanzmessung an.
9.4.2. Manhattan-Distanz#
Es gibt aber auch andere Möglichkeiten, den Abstand zwischen zwei Punkten zu definieren. Eine bekannte Alternative ist die sogenannte Manhattan-Distanz, bei der man einfach die Abstände in den einzelnen Dimensionen aufaddiert:
Hinweis: Der Betrag ist wichtig, weil wir nur positive Distanzen haben wollen, die sich zu einer Gesamtsumme aufaddieren und nicht etwa gegenseitig aufheben.
def manhattan_distanz(tier1: Tier, tier2: Tier) -> float:
d_niedlichkeit = abs(tier1.niedlichkeit - tier2.niedlichkeit)
d_flauschigkeit = abs(tier1.flauschigkeit - tier2.flauschigkeit)
distanz = d_niedlichkeit + d_flauschigkeit
return distanz
9.5. Programmierung des Algorithmus (2)#
9.5.1. Die \(k\) nächsten Nachbarn bestimmen#
# Wir sammeln die Distanzen aller bekannten Tiere (gelabelten Daten) zum unbekannten Tier (ungelabelter Datensatz).
# In dieser Fassung machen wir das möglichst einfach und nachvollziehbar, ohne fortgeschrittene Python-Features.
def berechne_manhattan_distanzen(ungelabelt: Tier, gelabelte_daten: list[Tier]) -> list[tuple[float, Tier]]:
distanzen = []
for tier in gelabelte_daten:
distanz = manhattan_distanz(ungelabelt, tier)
tupel = (distanz, tier) # Wir müssen uns die Distanz, aber auch das Tier merken (wichtig für die spätere Zuordnung nach dem Sortieren)
distanzen.append(tupel)
return distanzen
# Anwendung auf unsere Beispiel-Daten
manhattan_distanzen = berechne_manhattan_distanzen(unbekanntes_tier, tiere)
print("Unsortierte Distanzen:", manhattan_distanzen)
# Wir wollen die unserem unbekannten Tier am nächsten liegenden Tiere finden, also sortieren wir die Liste
manhattan_distanzen.sort() # Sortiert wird nach dem ersten Element des Tupels, also der Distanz
print("Sortierte Distanzen:", manhattan_distanzen)
def k_naechste_nachbarn(k: int, distanzen: list[tuple[float, Tier]]) -> list[Tier]:
k_nachbarn = []
for i in range(k):
distanz, tier = distanzen[i]
k_nachbarn.append(tier) # Jetzt interessiert uns nur noch das Tier, nicht mehr die Distanz
return k_nachbarn
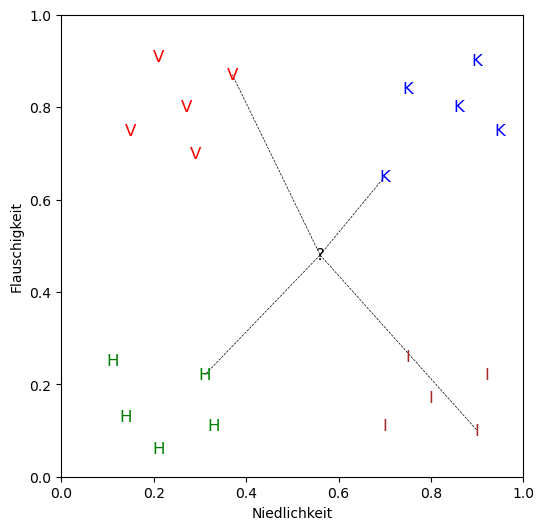
k = 5
k_nachbarn = k_naechste_nachbarn(k, manhattan_distanzen)
print(f"Die {k} nächsten Nachbarn sind: {k_nachbarn}")
plotte_daten(tiere, unbekanntes_tier, k_nachbarn)
Unsortierte Distanzen: [(0.7800000000000001, Tier(0.21, 0.91, 'vogelspinne')), (0.6100000000000001, Tier(0.27, 0.8, 'vogelspinne')), (0.68, Tier(0.15, 0.75, 'vogelspinne')), (0.5800000000000001, Tier(0.37, 0.87, 'vogelspinne')), (0.49000000000000005, Tier(0.29, 0.7, 'vogelspinne')), (0.76, Tier(0.9, 0.9, 'kaninchen')), (0.62, Tier(0.86, 0.8, 'kaninchen')), (0.5499999999999999, Tier(0.75, 0.84, 'kaninchen')), (0.6599999999999999, Tier(0.95, 0.75, 'kaninchen')), (0.30999999999999994, Tier(0.7, 0.65, 'kaninchen')), (0.51, Tier(0.31, 0.22, 'hai')), (0.77, Tier(0.14, 0.13, 'hai')), (0.77, Tier(0.21, 0.06, 'hai')), (0.68, Tier(0.11, 0.25, 'hai')), (0.6000000000000001, Tier(0.33, 0.11, 'hai')), (0.72, Tier(0.9, 0.1, 'igel')), (0.5499999999999999, Tier(0.8, 0.17, 'igel')), (0.5099999999999999, Tier(0.7, 0.11, 'igel')), (0.4099999999999999, Tier(0.75, 0.26, 'igel')), (0.62, Tier(0.92, 0.22, 'igel'))]
Sortierte Distanzen: [(0.30999999999999994, Tier(0.7, 0.65, 'kaninchen')), (0.4099999999999999, Tier(0.75, 0.26, 'igel')), (0.49000000000000005, Tier(0.29, 0.7, 'vogelspinne')), (0.5099999999999999, Tier(0.7, 0.11, 'igel')), (0.51, Tier(0.31, 0.22, 'hai')), (0.5499999999999999, Tier(0.8, 0.17, 'igel')), (0.5499999999999999, Tier(0.75, 0.84, 'kaninchen')), (0.5800000000000001, Tier(0.37, 0.87, 'vogelspinne')), (0.6000000000000001, Tier(0.33, 0.11, 'hai')), (0.6100000000000001, Tier(0.27, 0.8, 'vogelspinne')), (0.62, Tier(0.92, 0.22, 'igel')), (0.62, Tier(0.86, 0.8, 'kaninchen')), (0.6599999999999999, Tier(0.95, 0.75, 'kaninchen')), (0.68, Tier(0.11, 0.25, 'hai')), (0.68, Tier(0.15, 0.75, 'vogelspinne')), (0.72, Tier(0.9, 0.1, 'igel')), (0.76, Tier(0.9, 0.9, 'kaninchen')), (0.77, Tier(0.21, 0.06, 'hai')), (0.77, Tier(0.14, 0.13, 'hai')), (0.7800000000000001, Tier(0.21, 0.91, 'vogelspinne'))]
Die 5 nächsten Nachbarn sind: [Tier(0.7, 0.65, 'kaninchen'), Tier(0.75, 0.26, 'igel'), Tier(0.29, 0.7, 'vogelspinne'), Tier(0.7, 0.11, 'igel'), Tier(0.31, 0.22, 'hai')]
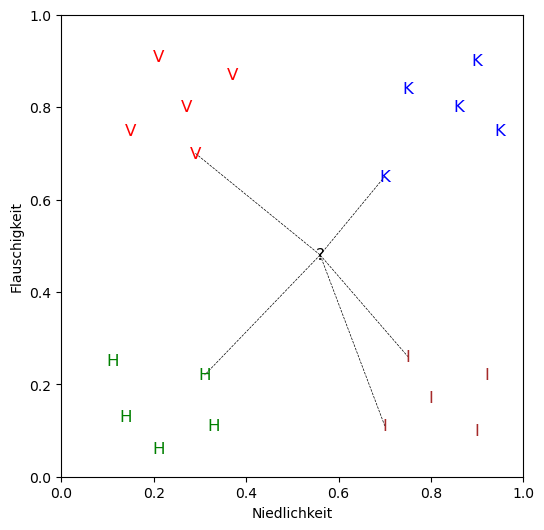
9.5.2. Eine “Abstimmung” unter den nächsten Nachbarn durchführen#
def haeufigkeiten_ermitteln(nachbarn: list[Tier]) -> dict[str, int]:
haeufigkeiten: dict[str, int] = {} # In diesem assoziativen Array (Dictionary) zählen wir, wie oft jede Spezies in den k nächsten Nachbarn vorkommt
for tier in nachbarn:
spezies = tier.spezies
if spezies not in haeufigkeiten:
haeufigkeiten[spezies] = 1 # Erster Eintrag für diese Spezies
else:
haeufigkeiten[spezies] += 1 # Schon bekannt, also Zähler erhöhen
return haeufigkeiten
# Anwendung auf unsere Beispieldaten
haeufigkeiten = haeufigkeiten_ermitteln(k_nachbarn)
print("Häufigkeiten der Spezies:", haeufigkeiten)
Häufigkeiten der Spezies: {'kaninchen': 1, 'igel': 2, 'vogelspinne': 1, 'hai': 1}
# Wir wählen die Spezies mit der höchsten Häufigkeit
def haeufigsten_wert_ermitteln(haeufigkeiten: dict[str, int]) -> str:
haeufigste_spezies: str = ""
max_h = 0
for spezies in haeufigkeiten:
h = haeufigkeiten[spezies]
if h > max_h:
haeufigste_spezies = spezies
max_h = h
return haeufigste_spezies
# Anwendung auf unsere Beispieldaten
haeufigste_spezies = haeufigsten_wert_ermitteln(haeufigkeiten)
print(f"Als Ergebnis des k-NN-Algorithmus ergibt sich für das unbekannte Tier {unbekanntes_tier} die Spezies:")
print(haeufigste_spezies)
# Passt das Ergebnis zu den k nächsten Nachbarn?
klassifiziertes_tier = unbekanntes_tier.kopie_mit_spezies(haeufigste_spezies)
plotte_daten(tiere, klassifiziertes_tier, k_nachbarn)
Als Ergebnis des k-NN-Algorithmus ergibt sich für das unbekannte Tier Tier(0.56, 0.48, '?') die Spezies:
igel
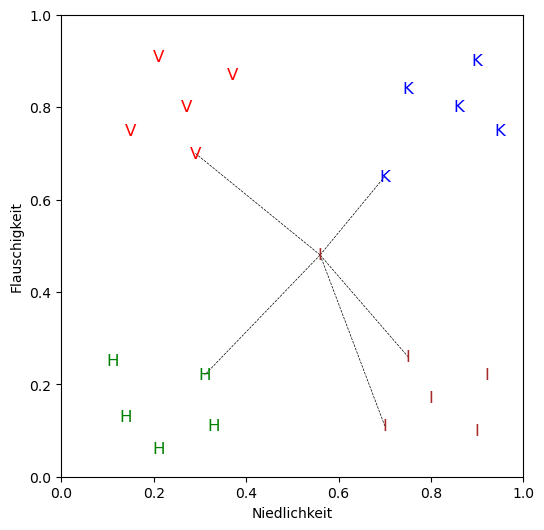
9.5.3. Der Algorithmus als Ganzes#
# Wir fassen die bisherigen Schritte in einer Funktion zusammen
def k_naechste_nachbarn_bestimmen(unbekanntes_tier: Tier, gelabelte_daten: list[Tier], k: int) -> tuple[str, list[Tier]]:
""" Bestimmt die k nächsten Nachbarn eines unbekannten Tiers und deren häufigste Spezies.
Parameter:
unbekanntes_tier (Tier): Das Tier, dessen Spezies bestimmt werden soll.
gelabelte_daten (list[Tier]): Liste von Tieren mit bekannten Spezies.
k (int): Anzahl der nächsten Nachbarn.
Rückgabe:
tuple[str, list[Tier]]: Die häufigste Spezies und die k nächsten Nachbarn. """
distanzen: list[tuple[float, Tier]] = berechne_manhattan_distanzen(unbekanntes_tier, gelabelte_daten)
distanzen.sort()
k_nachbarn = k_naechste_nachbarn(k, distanzen)
haeufigkeiten = haeufigkeiten_ermitteln(k_nachbarn)
spezies = haeufigsten_wert_ermitteln(haeufigkeiten)
return spezies, k_nachbarn # Wir geben auch die k nächsten Nachbarn zurück, damit wir sie später visualisieren können
9.5.4. Einige Beispiele#
def klassifiziere_und_plotte(test_tier: Tier, tiere: list[Tier], k: int) -> None:
spezies, k_nachbarn = k_naechste_nachbarn_bestimmen(test_tier, tiere, k)
print(f"Das unbekannte Tier {test_tier} wird klassifiziert als: {spezies}")
klassifiziertes_tier = test_tier.kopie_mit_spezies(spezies)
plotte_daten(tiere, klassifiziertes_tier, k_nachbarn)
test_tier = Tier(niedlichkeit=0.56, flauschigkeit=0.68, spezies="?")
k = 5 # Probiere auch andere kleine oder große Werte
klassifiziere_und_plotte(test_tier, tiere, k)
Das unbekannte Tier Tier(0.56, 0.68, '?') wird klassifiziert als: vogelspinne
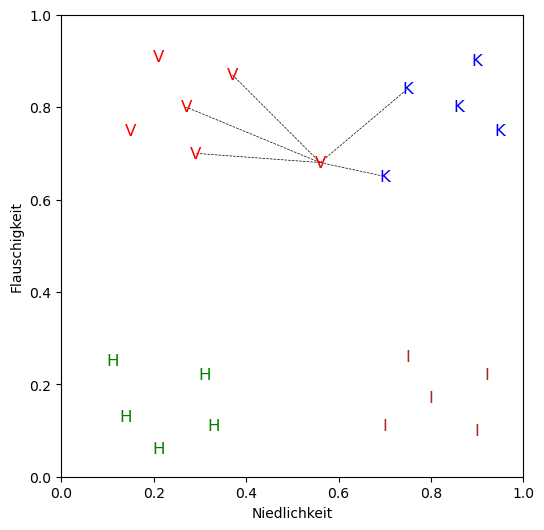
test_tier = Tier(niedlichkeit=0.36, flauschigkeit=0.48, spezies="?")
k = 3 # Probiere mal k=7 und andere kleine oder große Werte
klassifiziere_und_plotte(test_tier, tiere, k)
Das unbekannte Tier Tier(0.36, 0.48, '?') wird klassifiziert als: hai
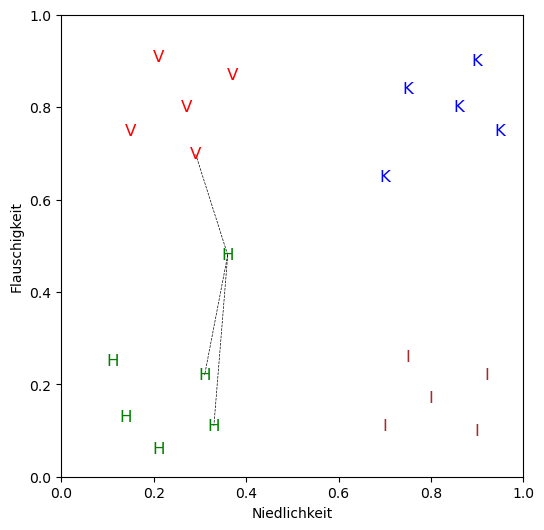
Das nächste Beispiel führt zu einem etwas unbefriedigenden Ergebnis… Findest du nicht auch?
test_tier = Tier(niedlichkeit=0.56, flauschigkeit=0.48, spezies="?")
k = 3
klassifiziere_und_plotte(test_tier, tiere, k)
Das unbekannte Tier Tier(0.56, 0.48, '?') wird klassifiziert als: kaninchen