Binärbäume

Inhalt

6.4. Binärbäume#

6.4.1. Einführung#

Im vorigen Kapitel haben wir allgemeine Bäume mit beliebig vielen Kindern betrachtet. In diesem Kapitel schauen wir uns den Spezialfall Binärbaum genauer an. Zur Erinnerung:

Definition

Ein Binärbaum ist ein Baum, bei dem jeder Knoten maximal zwei Nachfolger hat.

Wie du schon in Abb. 6.6 gesehen hast:

Wichtig

Die Teile eines Baums sind selbst wieder Bäume (Teilbäume).

Z.B. ist in der folgenden Abb. 6.9

der Knoten “Tier” die Wurzel des gesamten Baums, aber auch
der Knoten “Säugetier” die Wurzel des linken Teilbaums und
der Knoten “Fisch” die Wurzel des rechten Teilbaums.

../_images/s%C3%A4ugetiere_15knoten.svg — Abb. 6.9 Binärbaum mit verschiedenen Säugetier-Kategorien#

6.4.2. Aufgaben#

Betrachte den Baum in Abb. 6.10 und beantworte dann die folgenden Fragen:

../_images/aufgabe_binbaum_zahlen.svg — Abb. 6.10 Ein Binärbaum voller Zahlen#

Handelt es sich bei hier um einen binären Suchbaum?

Nein, es ist zwar ein binärer Baum, aber kein binärer Suchbaum.

Welche Knoten (inkl. Blätter) enthält der rechte Teilbaum des Knotens 1?

6, 9, 10, 11

Welche Knoten haben keinen rechten Teilbaum?

Die inneren Knoten 2 und 9 (und natürlich alle Blätter, d.h. 5, 7, 8, 10, 11)

Hat Knoten 9 einen linken oder einen rechten Teilbaum?

Knoten 9 hat einen linken Teilbaum.

Welche Knoten (inkl. Blätter) hat der linke Teilbaum des Knotens 2?

4, 7, 8

6.4.3. Umsetzung in Python#

Aber wie programmiert man einen Binärbaum? Die Abbildungen in den vorigen Abschnitten sehen ja schon ziemlich furchteinflößend aus, nicht wahr?

Keine Sorge, so schlimm ist es nicht, denn tatsächlich besteht jeder noch so riesige Baum aus den immergleichen “Bausteinen”, den Knoten. Und die kennen wir ja eigentlich schon von den verketteten Listen.

Knoten#

Der Knoten ist der zentrale Baustein für Bäume (und ähnliche Strukturen, insb. Graphen). Ein Knoten speichert

einerseits einen beliebigen Inhalt, z.B. eine Zahl, einen Text, einen Ort, den Zustand eines Spielbretts, eine Verzweigungsbedingung (in einem Entscheidungsbaum) usw.
und anderseits Kanten zu weiteren Knoten. Diese stehen z.B. für Straßen zwischen Orten, Spielzüge (die von einem Spielzustand in einen anderen führen) oder irgendeine andere Beziehung zwischen dem jeweiligen Knoten und seinen Kindknoten.

Spezialfall Binärbaum: Da ein Binärbaum (maximal) zwei Kindknoten hat, einen linken und einen rechten, können wir eine einfache Knoten-Klasse so definieren:

class Knoten:
    def __init__(self, inhalt):
        self.inhalt = inhalt  # Ein beliebiger Inhalt (d.h. eine Zahl, ein String, ein anderes Objekt, ...)
        self.linker_teilbaum: Knoten|None = None    # Verweis auf den Knoten, der als Wurzel des linken Teilbaums dient
        self.rechter_teilbaum: Knoten|None = None   # Verweis auf den Knoten, der als Wurzel des rechten Teilbaums dient

    def __str__(self):
        """Knoten in Textform ausgeben"""
        return f"Knoten({self.inhalt}, L:{self.linker_teilbaum}, R:{self.rechter_teilbaum})"

Das sieht doch wirklich recht ähnlich aus wie bei einer verketteten Liste… nur dass wir statt eines einzigen Verweis naechster auf den Nachfolgeknoten in der Liste jetzt Verweise auf zwei Nachfolgerknoten haben, linker_teilbaum und rechter_teilbaum.

Um zu verstehen, wie aus einer so einfachen Datenstruktur ein komplexes Gebilde wie der Baum aus Abb. 6.12 entstehen kann, bauen wir dieses Beispiel einfach in Python nach:

../_images/s%C3%A4ugetiere_7tiere.svg — Abb. 6.12 Dieser Baum enthält zahlreiche Knoten (naja, sieben)#

# Wir legen den ersten Knoten an und speichern ihn in der Variablen wurzel
wurzel = Knoten("Säugetier")
# Wir legen weitere Knoten an
k2 = Knoten("Hund")
k3 = Knoten("Collie")
k4 = Knoten("Dackel")
k5 = Knoten("Affe")
k6 = Knoten("Schimpanse")
k7 = Knoten("Orang-Utan")
# Das ist die entscheidende Stelle: Wir verknüpfen die Knoten miteinander
wurzel.linker_teilbaum = k2  # k2 (Hund) wird als linker Teilbaum an wurzel (Säugetier) angehängt 
k2.linker_teilbaum = k3  # k3 (Collie) wird als linker Teilbaum an k2 (Hund) angehängt
k2.rechter_teilbaum = k4  # usw.
wurzel.rechter_teilbaum = k5
k5.linker_teilbaum = k6
k5.rechter_teilbaum = k7

# Ausgabe der Struktur (Achtung: Das wird eine lange, unübersichtliche Textzeile)
print(wurzel)

Knoten(Säugetier, L:Knoten(Hund, L:Knoten(Collie, L:None, R:None), R:Knoten(Dackel, L:None, R:None)), R:Knoten(Affe, L:Knoten(Schimpanse, L:None, R:None), R:Knoten(Orang-Utan, L:None, R:None)))

6.4.4. Mit Bäumen Sachen machen#

Natürlich wollen wir Bäume nicht nur erstellen, sondern mit ihnen arbeiten. Zum Beispiel wollen wir

alle Inhalte des Baums ausgeben
die Knoten (oder Kanten oder Blätter) eines Baums zählen
etwas (schnell) in einem Baum finden
alle Inhalte eines Baums miteinander verrechnen (wenn es sich um Zahlen handeln)
oder die Inhalte eines Baums auf eine andere Art zu etwas Neuem kombinieren (z.B. so wie bei dem “Rechenbaum” aus Abb. 6.4)

Für alle diese Aufgaben benötigen wir Rekursion. Was das ist, erfährst du jetzt. Wir beginnen mit der Frage, was es eigentlich bedeutet, die in einem Baum gespeicherten Inhalte auszugeben.

Alle Inhalte eines Baums ausgeben#

Bei einer verketteten Liste ist die Reihenfolge der Elemente klar. Man gibt alle gespeicherten Werte aus, indem man beim ersten Knoten (dem Listenkopf) startet und sich dann von Nachfolger zu Nachfolger bewegt. Dabei gibt man jeweils den Wert im aktuellen Knoten aus.

Aber wie ist das bei Bäumen? Gibt es auch da eine “natürliche” Reihenfolge? Nein! Um das zu verstehen, betrachten wir das folgende Beispiel.

../_images/baum3einarmiger_bandit.svg — Abb. 6.13 Ein Baum mit drei Knoten. In welcher Reihenfolge würdest du sie ausgeben?#

Dieser Baum hat drei Knoten. Will man die drei darin gespeicherten Werte ausgeben, gibt es mehrere mögliche Reihenfolgen:

🍒 🍋 🔔 : Hier wurde die Wurzel vor den Kindern ausgegeben (Preorder-Reihenfolge).
🍋 🔔 🍒 : Hier wurde die Wurzel nach den Kindern ausgegeben (Postorder-Reihenfolge).
🍋 🍒 🔔 : Hier wurde die Wurzel zwischen den Kindern ausgegeben (Inorder-Reihenfolge).
(Theoretisch ergeben sich weitere drei Möglichkeiten, wenn man die Kinderknoten von rechts nach links statt von links nach rechts durchläuft. In der Praxis kommt das aber nur selten vor und wir ignorieren es hier deshalb einfach.)

Jede dieser Reihenfolgen kann bei bestimmten Anwendungen sinnvoll sein. Es wird allerdings leider etwas komplizierter, wenn der Baum größer ist…

../_images/baum7buchstaben.svg — Abb. 6.14 Ein Baum mit sieben Knoten.#

Was bedeuten Preorder, Postorder und Inorder in diesem Fall?

Preorder: Die Wurzel wird vor den beiden Teilbäumen ausgegeben, d.h. zuerst wird die Wurzel, dann der linke Teilbaum und zum Schluss der rechte Teilbaum ausgegeben - und zwar beide Teilbäume ebenfalls in Preorder-Reihenfolge!
Postorder: Die Wurzel wird nach den beiden Teilbäumen ausgegeben. Auch hier werden die Teilbäume ebenfalls in Postorder-Reihenfolge ausgegeben.
Inorder: Die Wurzel wird zwischen den beiden Teilbäumen ausgegeben, d.h. nachdem der linke und bevor der rechte Teilbaum ausgegeben wurde. Natürlich werden auch hier die beiden Teilbäume - wie der Gesamtbaum - in Inorder-Reihenfolge durchlaufen und ausgegeben.

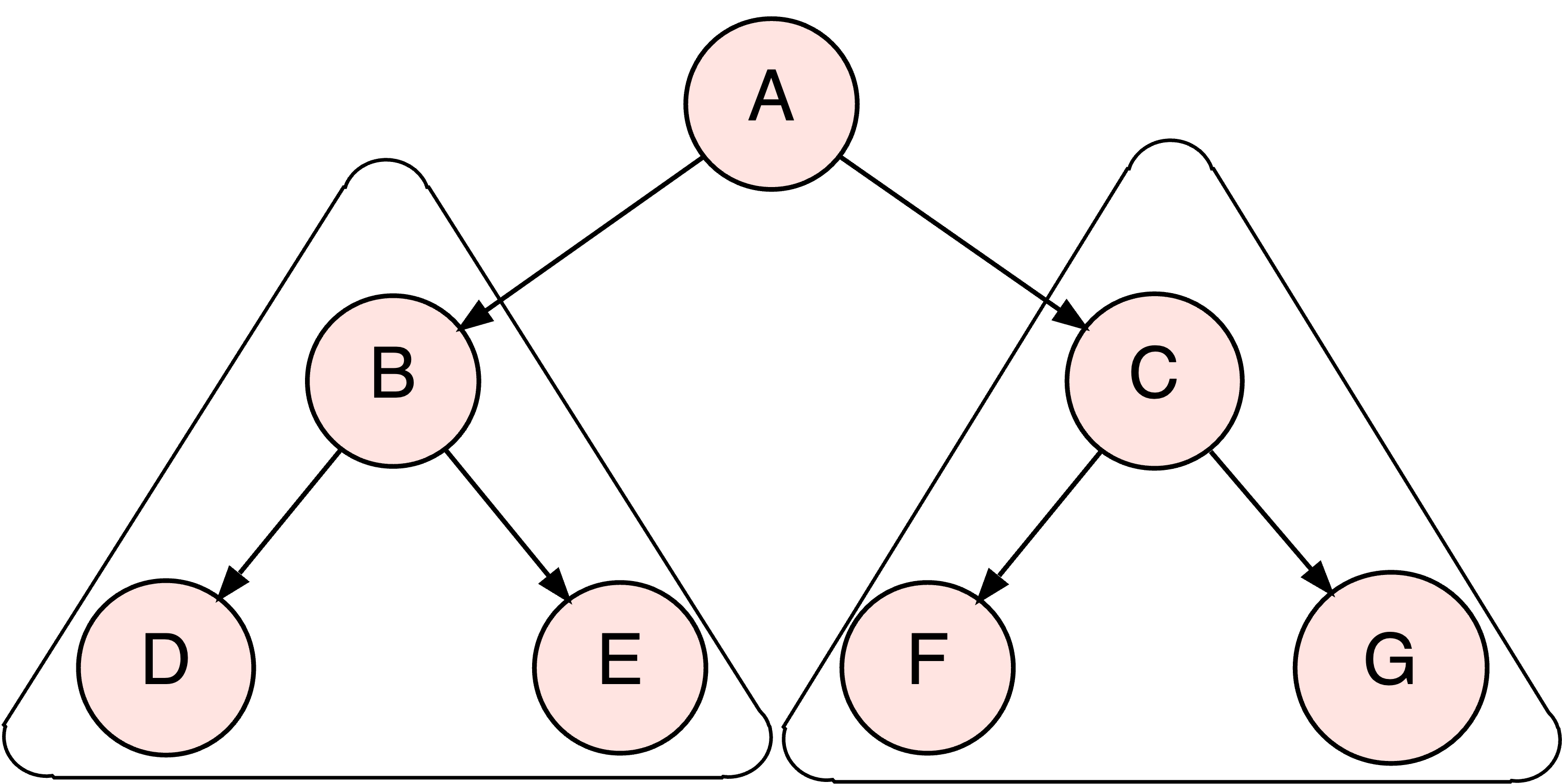
../_images/teilb%C3%A4ume.png — Abb. 6.15 Der Gesamtbaum hat 7 Knoten. Er besteht aus einer Wurzel und zwei Teilbäumen mit je 3 Knoten.#

Für unseren Beispiel-Baum bedeutet das konkret:

Preorder: Zuerst wird die Wurzel des Gesamtbaums (A) ausgegeben, dann “steigt” man in den linken Teilbaum und wiederholt für diesen das Verfahren:
- Zuerst gibt man die Wurzel aus (B), dann “steigt” man in den linken Teilbaum und wiederholt für diesen das Verfahren:
  - Zuerst gibt man die Wurzel aus (D) - aber dann gibt es keinen linken Teilbaum mehr und auch keinen rechten. Also kehrt man auf die nächsthöhere Ebene zurück (zu B) und kann nun dessen rechten Teilbaum ausgeben:
  - Zuerst die Wurzel (E)… und dann gibt es (zum Glück) auch hier keine Kinder mehr. Damit ist der gesamte Teilbaum mit der Wurzel B ausgegeben.
- Man kehrt zurück zu A und kann endlich dessen rechten Teilbaum ausgeben…
Insgesamt ergibt sich als Preorder-Reihenfolge: A, B, D, E, C, F, G
Postorder: Hier werden die Wurzel erst nach den Teilbäumen ausgegeben. D.h. bevor A ausgegeben werden kann, muss man zuerst in den linken Teilbaum steigen.
- Dessen Wurzel (B) darf aber auch erst ausgegeben werden, wenn man mit Bs Teilbäumen fertig ist.
  - Da diese (D und E) aber keine Kinder haben, werden sie tatsächlich ausgegeben.
  - Danach die aktuelle Wurzel, also B.
- Es geht zurück zu A - das aber immer noch nicht ausgegeben werden darf, weil zuerst sein rechter Teilbaum abgearbeitet werden muss.
- Dessen Wurzel © darf aber auch erst ausgegeben werden, wenn man mit Cs Teilbäumen fertig ist.
  - Da diese (F und G) aber keine Kinder haben, werden sie tatsächlich ausgegeben.
  - Danach die aktuelle Wurzel, also C.
- Nun sind wir mit beiden Teilbäumen von A fertig und können ganz zum Schluss auch A ausgeben!
Insgesamt ergibt sich als Postorder-Reihenfolge: D, E, B, F, G, C, A
Inorder: Hier wird erst der linke Teilbaum, dann die Wurzel, dann der rechte Teilbaum abgearbeitet.
- Wir steigen also zuerst in den linken Teilbaum mit der Wurzel B. Bevor diese ausgegeben werden kann, muss aber ihr linker Teilbaum abgearbeitet worden sein, also
  - steigen wir nach links hinunter zum Teilbaum mit der Wurzel D. Da dies ein Blattknoten ist, können wir ihn ausgeben.
- Dann geht es zurück zur Wurzel dieses Teilbaums, also B, den wir ausgeben…
  - und hinunter in den rechten Teilbaum mit der Wurzel E. Da dies ein Blattknoten ist, können wir ihn ausgeben.
- Nun haben wir den gesamten Teilbaum unter B abgearbeitet. Das war der linke Teilbaum von A, so dass wir in der Inorder-Reihenfolge jetzt die Wurzel (A) ausgeben, bevor wir…
  - in den rechten Teilbaum © hinabsteigen, den wir auf dieselbe Weise ausgeben, also: links (F) vor Wurzel © vor rechts (G)
Insgesamt ergibt sich als Inorder-Reihenfolge: D, B, E, A, F, C, G

6.4.5. Aufgaben#

Aufgaben zur Preorder-, Inorder- und Postorder-Traversierung#

Aufgabe: Gib für die folgenden Bäume jeweils alle Elemente in

Preorder-
Postorder- und
Inorder-Reihenfolge

an.

a)

Lösung:

Preorder: 3, 2, 4, 7, 8, 1, 5, 6, 9, 11, 10
Postorder: 7, 8, 4, 2, 5, 11, 9, 10, 6, 1, 3
Inorder: 7, 4, 8, 2, 3, 5, 1, 11, 9, 6, 10

b)

Lösung:

Preorder: 58, 25, 24, 13, 12, 19, 39, 72, 60, 66, 61, 69, 76, 81, 79
Postorder: 12, 19, 13, 24, 39, 25, 61, 69, 66, 60, 79, 81, 76, 72, 58
Inorder: 12, 13, 19, 24, 25, 39, 58, 60, 61, 66, 69, 72, 76, 79, 81

c)

Lösung:

Preorder: !, D, R, I, H, I, S, E, R, P, S, U, E
Postorder: I, H, R, S, E, I, D, S, U, P, E, R, !
Inorder: I, R, H, D, S, I, E, !, S, P, U, R, E

Hast du alle Aufgaben gelöst? Dann herzlichen Glückwunsch!!!1

6.4.6. Umsetzung in (Pseudo-)Code. Rekursion#

Diesen Baum haben vorhin bereits in Preorder-, Postorder- und in Inorder-Reihenfolge ausgegeben, allerdings nur von Hand. Wie können wir das programmieren?

Für (z.B.) Preorder kann man den Algorithmus intuitiv so beschreiben:

OPERATION Baum B in Preorder-Reihenfolge ausgeben

Um einen (Teil-)Baum B in Preorder-Reihenfolge auszugeben

gib zuerst den Inhalt des Wurzelknotens von B aus
dann gib auf dieselbe Weise den linken Teilbaum von B aus (falls dieser überhaupt existiert)
dann gib auf dieselbe Weise den rechten Teilbaum von B aus (falls dieser überhaupt existiert)

Entscheidend ist hier das hervorgehobene “auf dieselbe Weise”: Wir delegieren eine Teilaufgabe an einen Teilbaum - und dieser wendet dieselbe Operation an, die wir gerade erst beschreiben! Das nennt man Rekursion.

Aber ist das überhaupt möglich/erlaubt/sinnvoll? Die Antwort auf alle diese Fragen ist ja! Was das intuitiv bedeutet, haben wir ja weiter oben schon gesehen und angewendet. Jetzt wirst du sehen, dass das auch in einem Programm funktioniert. Hier siehst du dasselbe Verfahren im Pseudocode der Formelsammlung:

Pseudocode

OPERATION ausgebenDatenPreorder() der Klasse Knoten

    inhalt.ausgebenDaten()

    WENN linkerKnoten != NICHTS   # Das ist die Abbruchbedingung!
        linkerKnoten.ausgebenDatenPreorder()   # Rekursiver Aufruf
    ENDE WENN 

    WENN rechterKnoten != NICHTS   # Das ist die Abbruchbedingung!
        rechterKnoten.ausgebenDatenPreorder()  # Rekursiver Aufruf
    ENDE WENN

In Python kann man das z.B. so umsetzen:

class Knoten:

    ...  # Attribute und andere Methoden

    def print_preorder(self):
        """Gibt die Daten des Baums in Preorder-Reihenfolge aus."""

        print(self.inhalt)

        if self.linker_teilbaum != None:            # Abbruchbedingung
            self.linker_teilbaum.print_preorder()   # Rekursiver Aufruf

        if self.rechter_teilbaum != None:           # Abbruchbedingung
            self.rechter_teilbaum.print_preorder()  # Rekursiver Aufruf

Wichtig

Rekursive Funktionen/Methoden sind immer nach einem ähnlichen Prinzip aufgebaut:

Es gibt eine oder mehrere Stellen, an denen sich die Funktion selbst wieder aufruft.
Bei dem rekursiven Aufruf wird das bisherige Aufrufargument verändert, so dass es “einfacher” wird. Was “einfacher” bedeutet, hängt von der jeweiligen Aufgabe ab, aber es geht immer darum, das Argument so zu verändern, dass es “näher” an einem “einfachen” Wert ist, bei dem die Rekursion abgebrochen werden kann.
Vor dem rekursiven Aufruf findet deshalb immer eine Fallunterscheidung statt:
- Falls schon ein base case erreicht ist (also so ein “einfacher” Fall, bei dem das Ergebnis klar ist), findet kein rekursiver Aufruf statt, sondern dieses Teilergebnis wird sofort zurückgegeben oder die Funktion beendet.
- Ansonsten wird der Wert des Parameters angepasst (“vereinfacht”) und die Funktion mit diesem angepassten Wert rekursiv erneut aufgerufen.

Bsp.: Beim Durchlaufen eines Baums ist der base case eigentlich immer, dass man ein Blatt erreicht hat oder zumindest, dass ein bestimmter Teilbaum nicht existiert, so dass an dieser Stelle kein rekursiver Aufruf mehr sinnvoll ist.

6.4.7. Aufgaben#

Oft sind rekursive Problemlösungen kurz und elegant (zumindest, wenn man das Prinzip erstmal kapiert hat 😉). Bei Bäumen ist es sogar so, dass Lösungen ohne Rekursion meistens extrem kompliziert werden!

Zur Wahrheit gehört aber auch, dass es viele Problemstellungen gibt, bei denen statt Rekursion auch eine simple Schleife verwendet werden kann. Man spricht dann von einem iterativen Ansatz.

Aufgabe 1#

Vergleiche die beiden folgenden Funktionen - beide bestimmen die Länge einer verketteten Liste.

Überlege dir jeweils, wie die Funktionen funktionieren, und erkläre es deiner Sitznachbarin,
Diskutiert insbesondere, wie in der rekursiven Version verschiedene Returnwerte miteinander verrechnet werden.
Worin unterscheiden und worin ähneln sich die beiden Funktionen?
Welche Variante findest du leichter zu programmieren?
In der nächsten Aufgabe wirst du das Grundprinzip der rekursiven Lösung von einer verketteten Liste auf Binärbäume übertragen. Was glaubst du, musst du dabei verändern?

# Rekursive Funktion, die die Länge einer verketteten Liste ermittelt
def anzahl_knoten_in_liste(knoten: Knoten) -> int:
    """Anzahl der Knoten im Baum ermitteln. Rekursive Variante"""
    if knoten == None:  # base case
        return 0
    else:  # rekursiver Fall
        zwischenergebnis = anzahl_knoten_in_liste(knoten.naechster)
        return 1 + zwischenergebnis
    
# Iterative Funktion, die die Länge einer verketteten Liste ermittelt
def anzahl_knoten_in_liste_mit_schleife(knoten: Knoten) -> int:
    """Anzahl der Knoten im Baum ermitteln. Iterative Variante, d.h. mit Schleife"""
    anzahl = 0
    while knoten != None:
        anzahl += 1
        knoten = knoten.naechster
    return anzahl

Aufgabe 2#

Weiter oben hatten wir diesen Baum in Python mithilfe der Klasse Knoten definiert:

Dazu hatten wir mehrere Knoten-Objekte erzeugt und miteinander über die Attribute linker_teilbaum und rechter_teilbaum verknüpft. Den Wurzelknoten hatten wir in der Variablen wurzel gespeichert:

print(wurzel)

Knoten(Säugetier, L:Knoten(Hund, L:Knoten(Collie, L:None, R:None), R:Knoten(Dackel, L:None, R:None)), R:Knoten(Affe, L:Knoten(Schimpanse, L:None, R:None), R:Knoten(Orang-Utan, L:None, R:None)))

Aufgabe: Vervollständige die untenstehende Funktion, so dass die Anzahl aller Knoten im Baum berechnet wird.

Achtung (1): Die Funktion soll nichts ausgeben, sondern nur per return-Befehl Zahlen zurückliefern. Diese kann man dann in einer Variablen speichern oder mit print() ausgeben usw., so wie im Test am Ende der Codezelle.

Achtung (2): Achte darauf, dass es sich hier nicht um eine Methode der Klasse Knoten handelt, sondern um eine Funktion, die ein Knoten-Objekt als Parameter erhält. Wenn du also rekursiv dieselbe Funktion noch einmal aufrufst, schreibst du nicht irgendein_knoten.anzahl_knoten_binaerbaum(), sondern anzahl_knoten_binaerbaum(irgendein_knoten)!2 (Genau so wird die Funktion auch im Test am Ende der Codezelle aufgerufen.)

def anzahl_knoten_binaerbaum(knoten: Knoten|None) -> int:
    """Anzahl der Knoten im Baum ermitteln."""

    # Tipp: Orientiere dich an der Funktion anzahl_knoten_in_liste aus der vorherigen Aufgabe und
    # überlege dir, wie du die Funktion anpassen musst, um sie für einen Binärbaum zu verwenden.
    ...
    
# Test
anzahlKnoten = anzahl_knoten_binaerbaum(wurzel)  # Erwartet: 7
print(anzahlKnoten) 

None

Lösung:

Aufgabe 3#

Dies ist eine Variante der vorigen Aufgabe: Statt aller Knoten sollst du jetzt nur die Blattknoten zählen, also diejenigen Knoten, deren linker und rechter Teilbaum nicht existieren.

def anzahl_blattknoten(knoten: Knoten|None) -> int:
    """Anzahl der Blattknoten im Baum ermitteln."""

    # Tipp: Die Lösung ist sehr ähnlich zur vorherigen Aufgabe. Du darfst allerdings nur 
    # diejenigen Knoten zählen, die keine Kinder haben.
    ...
    
# Test
anzahlKnoten = anzahl_blattknoten(wurzel)  # Erwartet: 4
print(anzahlKnoten)

None

Lösung:

Aufgabe 4#

Bestimme die Tiefe eines Binärbaums.

Zur Erinnerung: Die Tiefe eines Baums entspricht der Anzahl der Knoten im längsten Pfad des Baums. Allerdings ist für diese Aufgabe vielleicht eine andere Beschreibung hilfreicher. Du findest sie hinter dem folgenden Tipp. Vielleicht brauchst du den Tipp ja aber gar nicht - die Lösung ist (mal wieder) seeeehr ähnlich wie die aus Aufgabe 2 😉.

Tipp

Ein leerer Baum hat die Tiefe 0. Für alle anderen Bäume gilt: Ihre Tiefe ist um eins größer als die seines linken oder rechten Teilbaums - je nachdem, welcher von beiden die größere Tiefe hat. Anders gesagt: Die Tiefe ist um eins größer als die maximale Tiefe seiner beiden Teilbäume.

def tiefe_binaerbaum(knoten: Knoten) -> int:
    """Tiefe des Baums ermitteln."""

    # Tipp: siehe Aufgabenstellung.
    ...
    
# Test
tiefe = tiefe_binaerbaum(wurzel)  # Erwartet: 3
print(tiefe)

None

Lösung:

Aufgabe 5#

Schreibe eine Funktion enthält_element(knoten, gesuchter_wert), die den gesuchten Wert im Baum (ausgehend von knoten) sucht und True zurückgibt, wenn es einen Knoten gibt, dessen Inhalt der gesuchte Wert ist, und sonst False.

Diese Aufgabe ist etwas schwieriger als die vorigen. Das liegt daran, dass es eine gewisse “Ungleichheit” zwischen zwei Fällen gibt:

Wenn man den gesuchten Wert gefunden hat, kann man aufhören.
Aber wenn man in einem Knoten oder Teilbaum den Wert nicht gefunden hat, weiß man noch lange nicht, ob er nicht doch noch in einem anderen Teil des Baums vorkommt.

Die Aufgabe wird etwas leichter zu lösen, wenn man nicht versucht, die Suche frühzeitig zu beenden. Du findest deshalb unten zwei verschiedene Musterlösungen. Beide sind korrekt, aber die zweite ist deutlich effizienter!

def enthält_element(knoten, gesuchter_wert) -> bool:
    """Prüfen, ob der Baum ein bestimmtes Element enthält."""

    # Tipp: siehe Aufgabenstellung.
    ...
    
# Test
ergebnis = enthält_element(wurzel, "Collie")  # Erwartet: True
print(ergebnis)
ergebnis = enthält_element(wurzel, "Katze")  # Erwartet: False
print(ergebnis)

None
None

Lösung 1: Die folgende Lösung ist zwar korrekt, aber nicht besonders effizient, wenn der gesuchte Wert eigentlich schon früh gefunden wurde. Kannst du erklären, warum?

Lösung 2: Diese zweite Lösung ist viel effizienter, wenn der gesuchte Wert schon früh gefunden wird. Kannst du erklären, warum?

6.4.8. Die Klasse Binaerbaum#

Das folgende Klassendiagramm stammt aus der Formelsammlung. Du siehst

unsere altbekannte Klasse Knoten mit Referenzen auf den inhalt des Knotens sowie auf seinen linken Teilbaum (linkerKnoten) und rechten Teilbaum (rechterKnoten).
allerdings sind diese Referenzen jetzt privat, so dass Getter- und Setter-Methoden zur Verfügung gestellt werden müssen, um auf diese Attribute zugreifen zu können: gibInhalt, …, setzeRechtenKnoten.
Außerdem gibt es einige weitere Methoden, insb. ausgebenDatenInorder usw. Diese haben wir weiter oben als separate Funktionen programmiert, die wir gleich in Methoden der Klasse umwandeln und dabei leicht verändern müssen!

V.a. haben wir jetzt die Klasse Binaerbaum, d.h. den Abstrakten Datentyp, der alle “öffentlich” zugänglichen Operationen auf Binärbäumen bereitstellt, ohne dass die Nutzer etwas von Knoten, Teilbäumen oder Rekursion verstehen müssen. Wie die Arbeit intern verteilt wird, siehst du im untenstehenden Code.

../_images/BinBaum.svg — Abb. 6.17 Klassendiagramm Binärbaum aus der Formelsammlung#

Aufgabe: Vergleiche die Implementierung der Methoden anzahlKnoten, tiefe, enthaeltElement usw. mit den Lösungen aus dem vorigen Abschnitt.

Hinweise:

Die Implementierung ist generisch, d.h. jeder Knoten speichert einen bestimmten Typ von Daten, z.B. einen String, Integer oder eine selbstprogrammierte Klasse wie Person. Auch die VerketteteListe ist dann generisch: Eine VerketteteListe[int] kann nur int-Werte speichern, eine VerketteteListe[Tier] nur Tier-Objekte usw.
Das macht die Typ-Annotationen recht kompliziert. Für das Verständnis der Algorithmen sind diese auch nicht unbedingt notwendig - also ignoriere sie, wenn sie dich eher verwirren!

class Knoten[Typ]:  # ab Python 3.12 ist diese Schreibweise für generische Typen möglich

    def __init__(self, inhalt: Typ) -> None:
        self.__inhalt: Typ = inhalt
        self.__linkerKnoten: Knoten[Typ] | None = None
        self.__rechterKnoten: Knoten[Typ] | None = None

    def istBlatt(self) -> bool:
        return self.__linkerKnoten == None and self.__rechterKnoten == None

    def gibInhalt(self) -> Typ:
        return self.__inhalt

    def setzeInhalt(self, pInhalt: Typ) -> None:
        self.__inhalt = pInhalt

    def gibLinkenKnoten(self) -> Knoten[Typ] | None:
        return self.__linkerKnoten

    def setzeLinkenKnoten(self, pLinkerKnoten: Knoten[Typ]) -> None:
        self.__linkerKnoten = pLinkerKnoten

    def gibRechtenKnoten(self) -> Knoten[Typ] | None:
        return self.__rechterKnoten

    def setzeRechtenKnoten(self, pRechterKnoten: Knoten[Typ]) -> None:
        self.__rechterKnoten = pRechterKnoten


class Binaerbaum[Typ]:
    def __init__(self) -> None:
        self.__wurzel: Knoten[Typ] | None = None

    def gibWurzel(self) -> Knoten[Typ] | None:
        return self.__wurzel

    def setzeWurzel(self, pWurzel: Knoten[Typ]) -> None:
        self.__wurzel = pWurzel

    def istLeer(self) -> bool:
        return self.__wurzel == None

    def anzahlKnoten(self) -> int:
        # Dies ist die öffentliche Methode zur Ermittlung der Anzahl der Knoten im Baum.
        # Die eigentliche Arbeit wird von der privaten Methode __anzahlKnotenRekursiv erledigt.
        return self.__anzahlKnotenRekursiv(self.__wurzel)

    def __anzahlKnotenRekursiv(self, knoten: Knoten[Typ] | None) -> int:
        # private Hilfsmethode, die die Anzahl der Knoten im Baum rekursiv ermittelt.
        # Sie entspricht fast 1:1 der Funktion anzahl_knoten_binaerbaum aus von weiter oben.
        if knoten == None:
            return 0
        else:
            anzahlLinks = self.__anzahlKnotenRekursiv(knoten.gibLinkenKnoten())
            anzahlRechts = self.__anzahlKnotenRekursiv(knoten.gibRechtenKnoten())
            return 1 + anzahlLinks + anzahlRechts

    def anzahlBlaetter(self) -> int:
        # Diese Methode gibt die Anzahl der Blattknoten im Baum zurück.
        # Auch hier wird die eigentliche Arbeit von einer privaten Methode erledigt.
        return self.__anzahlBlaetterRekursiv(self.__wurzel)

    def __anzahlBlaetterRekursiv(self, knoten: Knoten[Typ] | None) -> int:
        # private Hilfsmethode, die die Anzahl der Blattknoten im Baum rekursiv ermittelt
        if knoten == None:
            return 0
        if knoten.istBlatt():
            return 1
        else:
            anzahlLinks = self.__anzahlBlaetterRekursiv(knoten.gibLinkenKnoten())
            anzahlRechts = self.__anzahlBlaetterRekursiv(knoten.gibRechtenKnoten())
            return anzahlLinks + anzahlRechts

    def tiefe(self) -> int:
        # Selbes Spiel wie oben: Die eigentliche Arbeit wird von einer privaten Methode erledigt.
        return self.__tiefeRekursiv(self.__wurzel)

    def __tiefeRekursiv(self, knoten: Knoten[Typ] | None) -> int:
        if knoten == None:
            return -1  # Die Tiefe eines leeren Baums ist -1; die der Wurzel ist 0‚
        else:
            tiefeLinks = self.__tiefeRekursiv(knoten.gibLinkenKnoten())
            tiefeRechts = self.__tiefeRekursiv(knoten.gibRechtenKnoten())
            return 1 + max(tiefeLinks, tiefeRechts)

    def enthaeltElement(self, gesuchterWert: Typ) -> bool:
        # Auch hier wird die eigentliche Arbeit von einer privaten Methode erledigt.
        return self.__enthaeltElementRekursiv(self.__wurzel, gesuchterWert)

    def __enthaeltElementRekursiv(
        self, knoten: Knoten[Typ] | None, gesuchterWert: Typ
    ) -> bool:
        # private Hilfsmethode, die prüft, ob ein bestimmtes Element im Baum enthalten ist
        if knoten == None:
            return False
        if knoten.gibInhalt() == gesuchterWert:
            return True
        linksGefunden = self.__enthaeltElementRekursiv(
            knoten.gibLinkenKnoten(), gesuchterWert
        )
        rechtsGefunden = self.__enthaeltElementRekursiv(
            knoten.gibRechtenKnoten(), gesuchterWert
        )
        if linksGefunden == True or rechtsGefunden == True:
            return True
        return False

# Tests
print("Binärbaum zum Speichern von Integer-Werten anlegen.")
baum = Binaerbaum[int]()  # Erzeugen eines leeren Baums, der Integer-Werte speichert
print("Ist der Baum leer?", baum.istLeer())  # Erwartet: True
print("Anzahl der Knoten im leeren Baum:", baum.anzahlKnoten())  # Erwartet: 0

k1: Knoten[int] = Knoten(1)
k2: Knoten[int] = Knoten(2)
k3: Knoten[int] = Knoten(3)
k4: Knoten[int] = Knoten(4)
k5: Knoten[int] = Knoten(5)
k6: Knoten[int] = Knoten(6)
k7: Knoten[int] = Knoten(7)

print("Wir fügen die Knoten 1 bis 7 ein.")
baum.setzeWurzel(k1)
k1.setzeLinkenKnoten(k2)
k1.setzeRechtenKnoten(k3)
k2.setzeLinkenKnoten(k4)
k2.setzeRechtenKnoten(k5)
k3.setzeLinkenKnoten(k6)
k3.setzeRechtenKnoten(k7)

anzahlKnoten = baum.anzahlKnoten()
print(f"Anzahl der Knoten ist jetzt: {anzahlKnoten}")  # Erwartet: 7

anzahlBlätter = baum.anzahlBlaetter()
print(f"Anzahl der Blattknoten ist: {anzahlBlätter}")  # Erwartet: 4

tiefe = baum.tiefe()  # Erwartet: 3
print(f"Die Tiefe des Baums ist: {tiefe}")

print("Enthält der Baum die Zahl 3?", baum.enthaeltElement(3))  # Erwartet: True
print("Enthält der Baum die Zahl 8?", baum.enthaeltElement(8))  # Erwartet: False

Binärbaum zum Speichern von Integer-Werten anlegen.
Ist der Baum leer? True
Anzahl der Knoten im leeren Baum: 0
Wir fügen die Knoten 1 bis 7 ein.
Anzahl der Knoten ist jetzt: 7
Anzahl der Blattknoten ist: 4
Die Tiefe des Baums ist: 2
Enthält der Baum die Zahl 3? True
Enthält der Baum die Zahl 8? False

def anzahlKnoten(knoten: Knoten[Typ] | None) -> int:
    if knoten == None:
        return 0
    else:
        anzahlLinks = anzahlKnoten(knoten.gibLinkenKnoten())
        anzahlRechts = anzahlKnoten(knoten.gibRechtenKnoten())
        return 1 + anzahlLinks + anzahlRechts

1: Aber hast du auch das easter egg gefunden?
2: Der Grund für die Verwendung einer allgemeinen Funktion statt einer Methode der Klasse Knoten ist, dass es damit leichter wird, den None-fall zu überprüfen. Der Parameter knoten kann jetzt auch None sein, so dass man den base case mit einer Abfrage à la if knoten == None: ... überprüfen kann.